SURABAYA— Dalam ilmu matematika, dikenal formulasi mekanika kuantum yang merupakan perkembangan dari formalisme matematika untuk teori yang menggunakan struktur matematika abstrak. Mengulik lebih dalam tentang peranan matematika dalam kuantum, Departemen Matematika Institut Teknologi Sepuluh Nopember (ITS) helat workshop bersama Prof Dr Drs Subiono MS.
Guru besar bidang Ilmu Aljabar Max Plus di Indonesia tersebut mengawali bahasannya tentang kalkulus kuantum yang dikenal sebagai kalkulus tanpa batas, bertujuan memberi pembaca wawasan dasar tentang kalkulus-q atau yang setara. Menurut Subiono, dalam beberapa tahun terakhir minat terhadap subjek ini telah menyebar. “Hal ini dikarenakan analisis-q telah membuktikan manfaatnya di berbagai bidang dan saat ini memiliki aplikasi yang luas di bidang-bidang penting seperti ilmu komputer dan fisika partikel, ” terangnya, Jum'at (1/4/2022).
Lanjutnya, pada teori aproksimasi, penerapan kalkulus-q merupakan area yang baru diterapkan dalam 25 tahun terakhir. Analog-q pertama dari polinomial Bernstein diperkenalkan oleh Alexandru Lupas pada 1987. Kemudian, ia menyampaikan bahwa terdapat beberapa hasil fundamental kalkulus-q telah ditemukan. “Ada aritmetika qubit, bit versus qubit, penyajian baku, keadaan qubit, dan lain sebagainya, ” ungkap lelaki asli Surabaya ini.
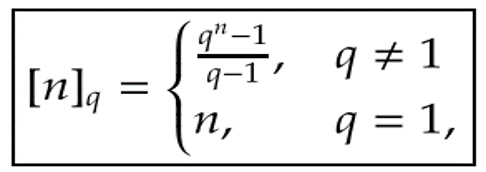
Rumus dari ilmu Kalkulus Kuantum yang dipaparkan oleh Prof Dr Drs Subiono MS
Dalam komputasi kuantum, bit kuantum atau qubit merupakan unit dasar informasi dari sebuah kuantum. Dimana versi kuantum dari bit biner klasik yang diwujudkan secara fisik dengan perangkat dua keadaan. Sekedar diketahui, penciptaan istilah qubit dapat dikaitkan dengan salah satu makalah tahun 1995 yang ditulis oleh Benjamin Schumacher. “Awalnya, istilah qubit ini dibuat sebagai bahan bercanda oleh penulis ketika berbicara dengan William Wootters, ” bebernya.
Doktor lulusan Delft University of Technology, Belanda tersebut menyampaikan bahwa dalam mekanika kuantum, keadaan kuantum umum dapat diwakili oleh superposisi linier dari dua keadaan basis ortonomalnya. Adapun keadaan basis qubit juga dapat digabungkan untuk membentuk keadaan hasil perkalian tensor basis. “Misalnya, dua qubit dapat disajikan dalam ruang vektor linier dimensi-empat yang dibentangkan oleh hasil perkalian tensor basis, ” jelasnya.
Selain itu, penggunaan matematika kuantum dapat diterapkan pada pemrosesan citra yang meneliti Representasi Gambar Kuantum yang Fleksibel (RGKF) untuk memperluas aplikasi pemrosesan gambar. Yakni, dari klasik (non-kuantum) ke domain komputasi kuantum. Prof Subiono berharap ilmu kuantum dapat semakin diaplikasikan ke bidang-bidang lainnya. “Penelitian mendatang akan meliputi kuantum finansial, pengelolaan citra, kriptografi atas Aljabar Max Plus yang diharapkan akan berguna ke depannya, ” pungkas Subiono dengan penuh harap. (*)
|
Baca juga:
GLS ITS Soroti Kesenjangan Upah Antar Gender
|
Reporter: Bima Surya Samudra
Redaktur: Astri Nawwar Kusumaningtyas


























